定积分

定义

概念

1. 分割：将总区域 $[a,b]$ 分割为 $n$ 个段，记 $\Delta x_k$ 为每一段的段间距（区域内需有界，分割可以不等间距）；

2. 近似：在每一段内任取一点 ${\delta }_k$，取该点处函数值 $f({\delta }_k)$ 作为矩形高度，并以当前段间距 $\Delta x_k$ 作为矩形宽度，计算每一块矩形面积;（可以不取端点）

3. 求和

4. 极限：让最大分割区域趋近于零：

${\lim }_{\lambda \to 0}{\sum }_{k=1}^{n}f({\delta }_k)\Delta x_k$

记 $\lambda =\max \left\{\Delta x_k\right\}$

若上一步求得的极限存在，且与分割方式以及 ${\delta }_k$ 的取法无关，则称：函数 $f(x)$ 在区间 $[a,b]$ 上可积。

${\int }_a^{b}f(x)\mathrm{d}x$

几何意义

1. 定积分 ${\int }_a^{b}f(x)\mathrm{d}x$ 就是计算曲线、直线 $x=a$ 、直线 $x=b$ 、x 轴围成的面积。

2. 在 x 轴上方为正，下方为负。总面积为上方面积减去下方面积。

精确定义

因为积分时存在两个 “任取” ，因此可以规定两个 “特取”：

1. 区间 $n$ 等分；
2. 取小区间右端点 ${\delta }_i$。

每段长度： ${\delta }_k=\frac{b-a}{n}$ 第 $i$ 点坐标： $a+\frac{b-a}{n}\cdot i$

$$\underset{n\to \infty }{\lim }\sum _n^{i=1}f\left(a+\frac{b-a}{n}i\right)\frac{b-a}{n}={\int }_a^{b}f(x)\mathrm{d}x$$

当 $a=0,b=1$ ：

重要 熟记

$$\underset{n\to \infty }{\lim }\sum _n^{i=1}f\left(\frac{i}{n}\right)\frac{1}{n}={\int }_0^{1}f(x)\mathrm{d}x$$

定积分的值与字母无关

$${\int }_a^{b}f(x)\mathrm{d}x={\int }_a^{b}f(t)\mathrm{d}t={\int }_a^{b}f(u)\mathrm{d}u$$

当定积分存在，定积分的值只和函数本身 $f(x)$ 与积分区间 $a,b$ 有关，与变量的记法无关。

面积是客观存在的量，不会因为记法而改变。

---

存在定理

也称为一元函数的（常义）可积性、黎曼可积性。

常义指“区间有限，函数有界”

定积分存在的充分条件

1. 若 $f(x)$ 在闭区间上连续，则积分存在；
2. 若 $f(x)$ 在闭区间上有界，且只有有限个间断点，则积分存在；
3. 若 $f(x)$ 在闭区间上单调，则积分存在。

自己的一些想法

定积分存在说明在该区域内可求面积，所以在该区域内必定有界，而连续函数必定有界且可求面积，对于第一类间断点，可以分成间断点两侧分别求面积，同样可求面积

Caution

1. 在后面提到 反常积分 （广义积分）时，函数无界也可能积分存在。但在常义可积时依然还是可积必有界。
2. 定积分存在定理与 不定积分存在定理 的区别与联系

定积分存在的必要条件

1. 闭区间是有限区间；
2. $f(x)$ 在闭区间内有界。

性质

两个规定

1. 当 $b=a$ 时： ${\int }_a^{b}f(x)\mathrm{d}x=0$ ;
2. 当 $a>b$ 时： ${\int }_a^{b}f(x)\mathrm{d}x=-{\int }_b^{a}f(x)\mathrm{d}x$ 。

性质 1：求区间长度

假设 $a<b$ ，则：

${\int }_a^{b}1\mathrm{d}x=b-a=L$

其中 $L$ 是区间 $[a,b]$ 的长度。

性质 2：积分的线性性质

$${\int }_a^b[k_{1}f(x)\pm k_{2}g(x)]\mathrm{d}x=k_1{\int }_a^{b}f(x)\mathrm{d}x\pm k_2{\int }_a^{b}g(x)\mathrm{d}x$$

性质 3：积分的可加（拆）性

无论 $a,b,c$ 大小如何，总有：

$${\int }_a^{b}f(x)\mathrm{d}x={\int }_a^{c}f(x)\mathrm{d}x+{\int }_c^{b}f(x)\mathrm{d}x$$

性质 4：积分的保号性

若在区间 $[a,b]$ 上 $f(x)\le g(x)$ ，则：

$${\int }_a^{b}f(x)\mathrm{d}x\le {\int }_a^{b}g(x)\mathrm{d}x$$

本身就小，面积也不会大

特殊地：有：

$$\left|{\int }_a^{b}f(x)\mathrm{d}x\right|\le {\int }_a^b\left|f(x)\right|\mathrm{d}x$$

Tip

事实上，只要区间内非负的 $f(x)$ 不恒等于零，那么其积分一定大于 0。

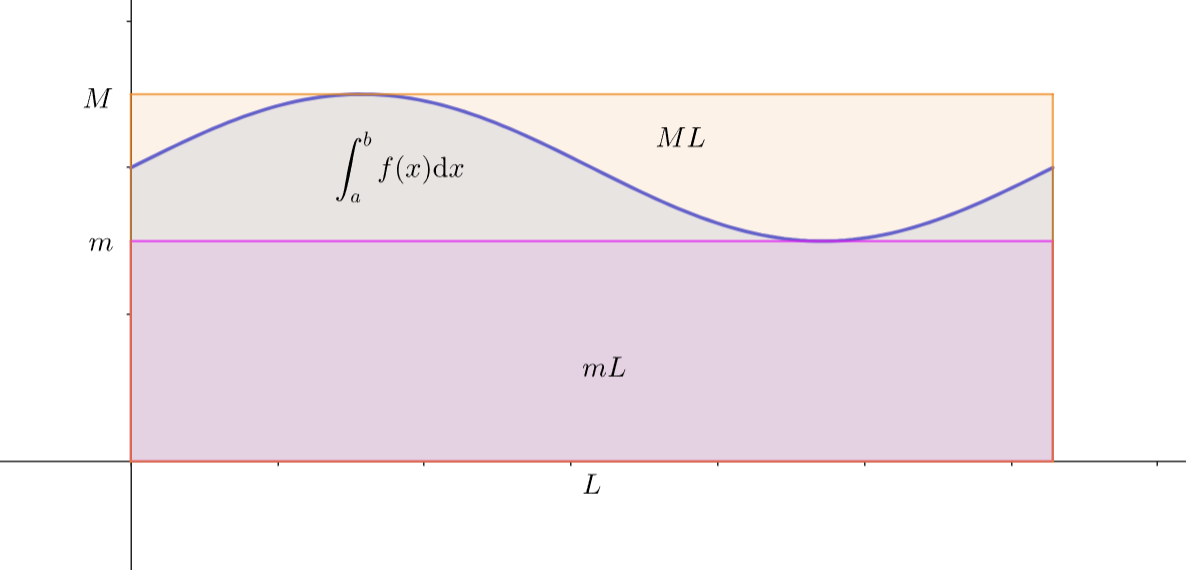
性质 5：估值定理

若 $f(x)$ 在区间 $[a,b]$ 有最值 $M,m$ ，设 $L$ 为区间长度，则有：

$$mL\le {\int }_a^{b}f(x)\mathrm{d}x\le ML$$

性质 6：中值定理

重要 又称为积分中值定理。

设 $f(x)$ 在闭区间连续，则在闭区间内至少存在一点 $\xi$ ，使得：

$${\int }_a^{b}f(x)\mathrm{d}x=f(\xi )(b-a)$$

证明

令 $F(x)={\int }_a^{x}f(t)\mathrm{d}t$ ，则 $F(x)$ 在 $[a,b]$ 上使用 7. 拉格朗日中值定理：

$$F(b)-F(a)=F^{\prime }(\xi )(b-a)$$

将 $F(b),F(a)$ 展开可得：

$${\int }_a^{b}f(x)\mathrm{d}x-0=f(\xi )(b-a),\xi \in (a,b)$$

Check

接下来请完成例 8.3 及之后的题目来巩固知识 :)

经典例题

数列和的极限

以下是两个经典的数列求和取极限的案例*（例 8.6）*，如何判别和解答呢？

Question

${\lim }_{n\to \infty }{\sum }_{i=1}^n\left(\frac{n+i}{n^2+i^2}\right)=?$

${\lim }_{n\to \infty }{\sum }_{i=1}^n\left(\frac{i}{n^2+n+i}\right)=?$

1. 开始之前

我们将此类数列和的极限记为：

$$\underset{n\to \infty }{\lim }\sum _{i=1}^{n}g(n,i)$$

其中 $g(n,i)$ 是数列通项，包含两个参数。

2. 判别是否符合精确定义

首先我们判别通项 $g(i,n)$ 是否能转化为 精确定义 中 $f(\frac{i}{n})\frac{1}{n}$ 的形式：

$$\underset{n\to \infty }{\lim }\sum _n^{i=1}f\left(\frac{i}{n}\right)\frac{1}{n}={\int }_0^{1}f(x)\mathrm{d}x$$

若分子或分母是关于 $n,i$ 的函数，且均为齐次式，则可以凑成 $f(\frac{i}{n})\frac{1}{n}$ 。

3.1 满足条件：使用定积分

如果满足条件，则直接使用定积分。 如：

$$\frac{n+i}{n^2+i^2}=\frac{n^2+in}{n^2+i^2}\cdot \frac{1}{n}=\frac{1+\frac{i}{n}}{1+(\frac{i}{n}{)}^2}\cdot \frac{1}{n}=f\left(\frac{i}{n}\right)\cdot \frac{1}{n}$$

又如：

$$\frac{1}{\sqrt{n^2+ni}}=\frac{1}{\sqrt{1+\frac{i}{n}}}\cdot \frac{1}{n}=f\left(\frac{i}{n}\right)\cdot \frac{1}{n}$$

后根据精确定义转化为积分计算及可，略。

3.2 不满足条件：使用夹逼

如果不满足条件，则考虑使用 夹逼准则 。如：

$$\underset{n\to \infty }{\lim }\sum _{i=1}^n\left(\frac{i}{n^2+n+i}\right)$$

将分母部分放缩到相同大小，对分子使用求和公式，再使用夹逼可得：

$$\frac{\frac{n(n+1)}{2}}{n^2+n+n}\le \sum _{i=1}^n\frac{i}{n^2+n+i}\le \frac{\frac{n(n+1)}{2}}{n^2+n+1}$$

抓大哥 $n^2$ 的系数：

$$\underset{n\to \infty }{\lim }\frac{\frac{n(n+1)}{2}}{n^2+n+n}=\underset{n\to \infty }{\lim }\frac{\frac{n(n+1)}{2}}{n^2+n+1}=\frac{1}{2}$$

大喊一声：哪里跑！

所以原式逼近到 $\frac{1}{2}$ 。

Caution

这两种方法不可互换。因此如果你在考试时发现其中一种方法算不出来，不要着急，马上换另一条路！

注意

Warning

$F(x)={\int }_a^{b}f(x,t)\mathrm{d}t$ 这个表达式不是定积分，是关于 $x$ 的函数。 定积分不是只看上下限，而是看整个是不是一个确定的常数！

Info

开始学习计算：定积分的计算