定积分的计算

牛顿-莱布尼茨公式及其推广

$F(x)$ 是 $f(x)$ 闭区间上的原函数，则：

${\int }_a^{b}f(x)\mathrm{d}x=F(x){|}_a^b=F(b)-F(a)$

Info

该定理联系了 不定积分 和 定积分。

但不代表不定积分和定积分只差了一个上下限。这只是形式上的相似。

证明

Tip

由于近几年考研数学对书上定义的考察愈加深刻。因此以防万一，在此给出其中一种证明。

记： $G(x)={\int }_a^{x}f(t)\mathrm{d}t(a\le x\le b)$

则可知：$G(b)={\int }_a^{b}f(x)\mathrm{d}x(G(a)=0)$

又因为： $F^{\prime }(x)=f(x)$ ，且 $G(x)=F(x)+C$

于是： ${\int }_a^{b}f(x)\mathrm{d}x=G(b)-G(a)=F(b)+C-(F(a)+C)=F(b)-F(a)$

得证。

推广

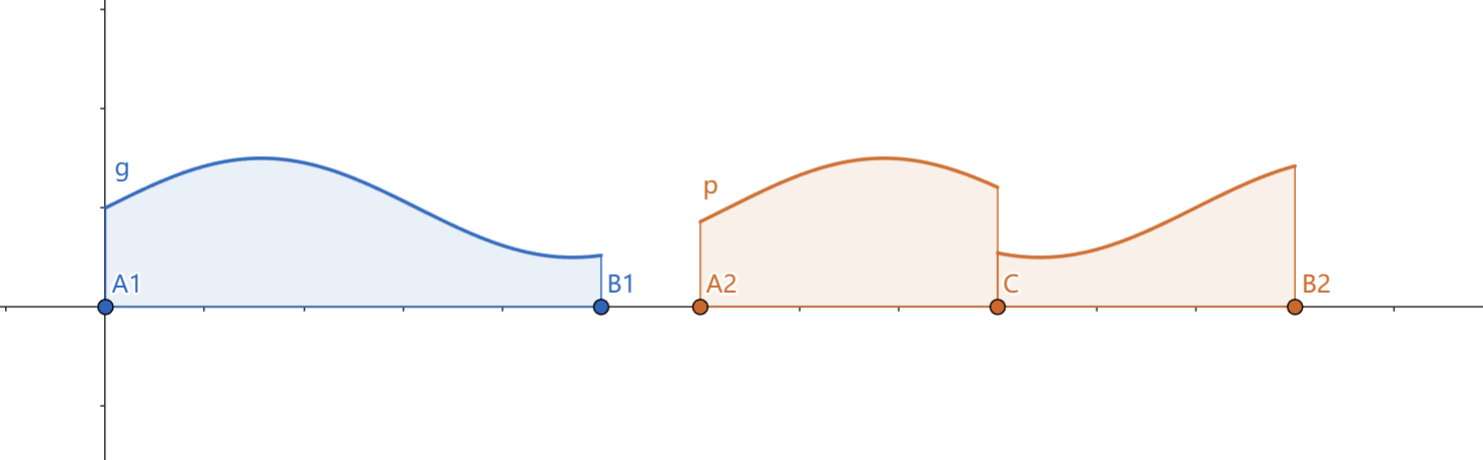
1. 若 $f(x)$ 在闭区间内有原函数： ${\int }_a^{b}f(x)\mathrm{d}x=F(b)-F(a)$
2. 若 $f(x)$ 在闭区间内有间断点 $c$： ${\int }_a^{b}f(x)\mathrm{d}x={\int }_a^{c}f(x)\mathrm{d}x+{\int }_c^{b}f(x)\mathrm{d}x$ 若 $c$ 点左右任意一边极限不存在，则积分发散。

Info

联系 不定积分的积分法 ，定积分有以下两种积分方法：

定积分的换元积分法

${\int }_a^{b}f(x)\mathrm{d}x={\int }_{\alpha }^{\beta }f[\phi (t)]{\phi }^{\prime }(t)\mathrm{d}t$

Tip

换元要三换：

• 被积函数换： $f(x)\to \phi (t)$
• 积分元素换： $\mathrm{d}x\to \mathrm{d}t$
• 上下限要换： ${\int }_a^b\to {\int }_{\alpha }^{\beta }$

定积分的分部积分法

${\int }_a^{b}u(x)v^{\prime }(x)\mathrm{d}x=u(x)v(x){|}_a^b-{\int }_a^b{u}^{\prime }(x)v(x)\mathrm{d}x$

要求二者导数在范围内连续。

重要结论

Note

以下是几个比较有用的结论：

奇偶性、周期性

• $f(x)$ 为连续偶函数，则： ${\int }_{-a}^{a}f(x)\mathrm{d}x=2{\int }_0^{a}f(x)\mathrm{d}x$
• $f(x)$ 为连续奇函数，则： ${\int }_{-a}^{a}f(x)\mathrm{d}x=0$
• $f(x)$ 周期为 $T$ ，则 ${\int }_a^{a+T}f(x)\mathrm{d}x={\int }_0^{T}f(x)\mathrm{d}x$ 一个周期长度的定积分，其值与起点位置无关。

区间再现公式

• $f(x)$ 连续，则： ${\int }_a^{b}f(x)\mathrm{d}x={\int }_a^{b}f(a+b-x)\mathrm{d}x$ 称作区间再现公式。证明见例 9.17

Example

${\int }_0^{\pi }xf(\sin x)dx=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)dx$

华里士公式

重要

华里士 (Wallis) 公式 可用于快速计算某些定积分！ ${\int }_0^{\frac{\pi }{2}}{\sin }^{n}x\mathrm{d}x={\int }_0^{\frac{\pi }{2}}{\cos }^{n}x\mathrm{d}x=\{\begin{array}{ll}\frac{n-1}{n}\times \frac{n-3}{n-2}\times \cdots \times \frac{2}{3}\times 1,& n为大于1的奇数\\ \frac{n-1}{n}\times \frac{n-3}{n-2}\times \cdots \times \frac{2}{3}\times \frac{\pi }{2},& n为正偶数\end{array}$

${\int }_0^{\pi }{\sin }^{n}x\mathrm{d}x=\{\begin{array}{ll}2\times \frac{n-1}{n}\times \frac{n-3}{n-2}\times \cdots \times \frac{2}{3}\times 1,& n为大于1的奇数\\ 2\times \frac{n-1}{n}\times \frac{n-3}{n-2}\times \cdots \times \frac{2}{3}\times \frac{\pi }{2},& n为正偶数\end{array}$ ${\int }_0^{\pi }{\cos }^{n}x\mathrm{d}x=\{\begin{array}{ll}0,& n为正奇数\\ 2\times \frac{n-1}{n}\times \frac{n-3}{n-2}\times \cdots \times \frac{2}{3}\times \frac{\pi }{2},& n为正偶数\end{array}$

${\int }_0^{2\pi }{\cos }^{n}x\mathrm{d}x={\int }_0^{2\pi }{\sin }^{n}x\mathrm{d}x=\{\begin{array}{ll}0,& n为正奇数\\ 4\times \frac{n-1}{n}\times \frac{n-3}{n-2}\times \cdots \times \frac{2}{3}\times \frac{\pi }{2},& n为正偶数\end{array}$ 如果从分母开始数，则数字部分非常像火箭发射倒计时，因此称其为点火公式。

Tip

若最后一位数的分子能数到 $1$ ，则可以点火（末尾乘 $\frac{\pi }{2}$ ）；若只能数到 $2$ ，则点火失败（不用乘系数）。

---

Note

定积分中许多情况下会用到换元： $x=\sin x$ 。换元后的上下限有多种情况都可以满足条件。

但被积函数中 $\sqrt{1-x^2}=\sqrt{1-{\sin }^{2}t}=|\cos t|$ 绝对值的处理有繁有简，应选取最合适的方法。

对于可积但不可求积的函数，详见 二重积分 待完善