Tip
10 大定理,无需证明直接用!!
涉及函数的定理
设 在 连续,则:
1. 有界与最值定理
,其中 分别为闭区间内最小值与最大值。
Summary
函数一定有界,且拥有最大最小值。
2. 介值定理
当 ,存在 ,使
Summary
最大最小值包裹的范围内,函数必经过其中每一个值。
在 之间画一条水平直线,其与函数至少有一个交点。
3. 平均值定理
当 时,在 内至少存在一点 ,使得:
提示
想象一个数轴,在 间插入 个点,则这 个插入点的平均值一定存在于 范围内。
4. 零点定理
当 时,存在 使 。
Summary
两点异号,中间必穿零点。
Tip
题目一般不会直接让你求证 ,往往需要经过一次逆运算,构造新的函数。(例 6.1)
推广
在 连续, , ,则 在 内至少有一个根。
Tip
可以是有限数,也可以是无限大。
涉及导数(微分)的定理
5. 费马定理
若函数在 满足:
- 可导;
- 取极值,
则 。
Tip
速度为 0 时跑得最远,加速度为 0 时跑得最快。
Info
导数零点定理
参考 4. 零点定理
例 6.3: 设 在 可导,若端点导数值异号,则 内必有一点导数为 。
Attention
请区分: 在闭区间可导 & 在闭区间连续。 函数可导:导函数存在,但不一定连续。
[!费马大定理]- :任何 ,一定没有正整数解。
我已经有了一个绝妙的证明,但是这里空间太小写不下了。
6. 罗尔定理
设函数 满足:
- 连续;
- 可导;
- ,
则:内部存在导数为 的点。
Info
Tip
看到 ,就想 5. 费马定理 或罗尔定理。
多次罗尔定理
设 ,
有 使:
再使用一次罗尔:有 使:

记住这个笑脸
罗尔定理推广
区间 可以是无穷区间;端点(极限)值可以是无穷大。
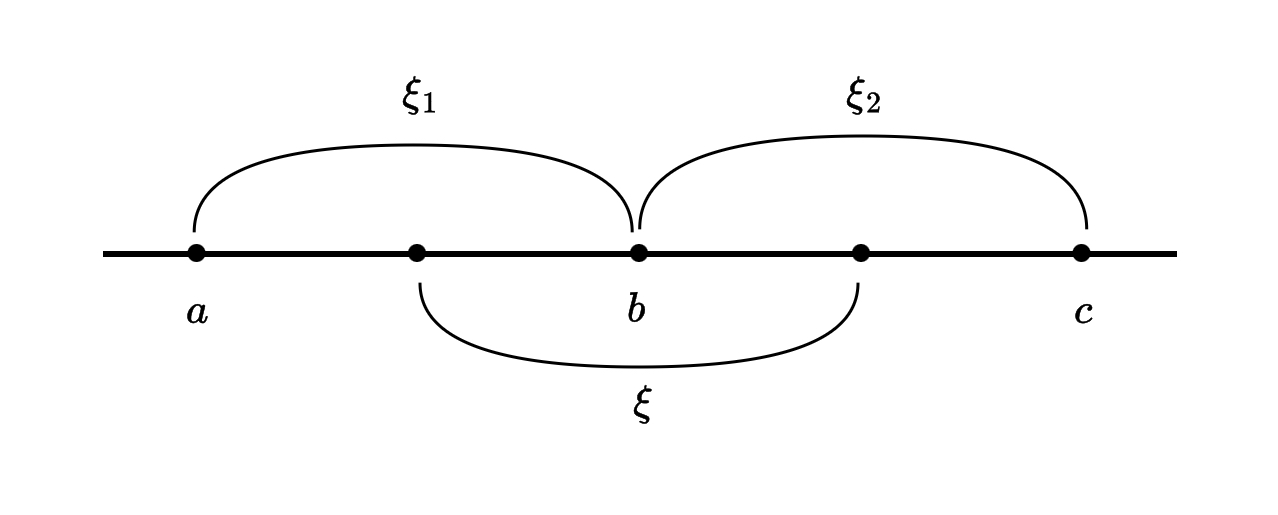
辅助函数
Note
考研主要侧重于简单构造,请勿过于沉迷构造辅助函数。
参考: 四则运算


Tip
- 注意广义化!
- 这些辅助函数不仅限于罗尔定理。
- 有的题目可能涉及到多次罗尔定理: ,三者中间有两点为 0,再对这两点使用罗尔可得二阶导为 0。
7. 拉格朗日中值定理
Tip
这个定理很简单,但是实际做题会有障碍。注意观察题目条件,来判断何时使用拉格朗日。
定理
设 满足:
- 连续;
- 可导,
则 间存在点 使:
或者写成:
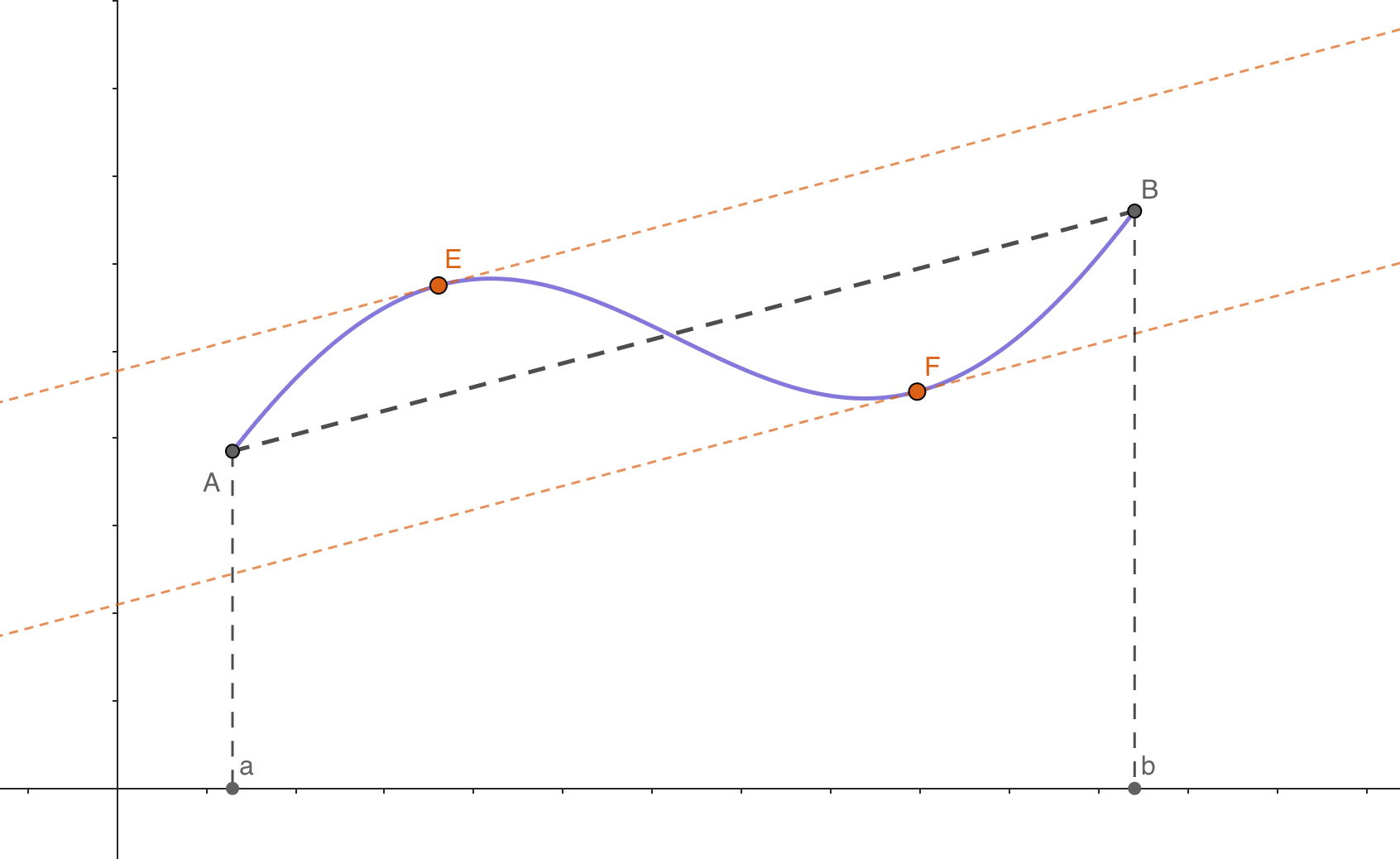
提示
注意看:这个拉格朗日的图像是不是和 6. 罗尔定理 有点相似?因为他们两个就是一样的!只是拉格朗日更加一般化。
见到 或者 与 的关系:想到拉格朗日中值定理。
例题
证明: 使
- 变形:
- 联想: 拉格朗日
- 发现:
- 正向书写:令 ,有
个人经验
在题目中,许多情况需要使用 这个条件简化拉格朗日中值定理。
可以将原式化为: 也可以直接将 替换为
8. 柯西中值定理
设 满足:
- 连续;
- 可导;
- ,
则存在 ,使
Tip
往往考察一个具体函数,一个抽象函数。
柯西中值定理其实也只是把 7. 拉格朗日中值定理 写成了参数方程的形式。
Caution
不能使用两个拉格朗日相除得到柯西!因为两个不同函数的 可能不相同!
9. 泰勒公式
Abstract
用多项式逼近/近似一个函数
带佩亚诺余项的 n 阶泰勒公式
Info
前置参考:导数的意义,一定要看!
Summary
将导数的一阶可导推广到了 n 阶可导。
适用于点 及其邻域,常用于研究点 的某些结论。(极限,无穷小阶数,极值)是局部的。
设 在点 处 阶可导,则存在 的一个邻域,对于邻域内任意点 有:
Tip
这个余项和之前的导数、连续一样,但是变成了 阶
带拉格朗日余项的 n 阶泰勒公式
Summary
升级到了 阶
适用于区间 ,常在证明题中使用(不等式、中值定理)
设 在点 某个邻域 阶导数存在,对邻域内任意点 有:
Tip
这个余项就是之前的通项,只不过将 替换为了介于 之间的 。
麦克劳林公式
当 时的泰勒公式称为麦克劳林公式。
重要麦克劳林展开式
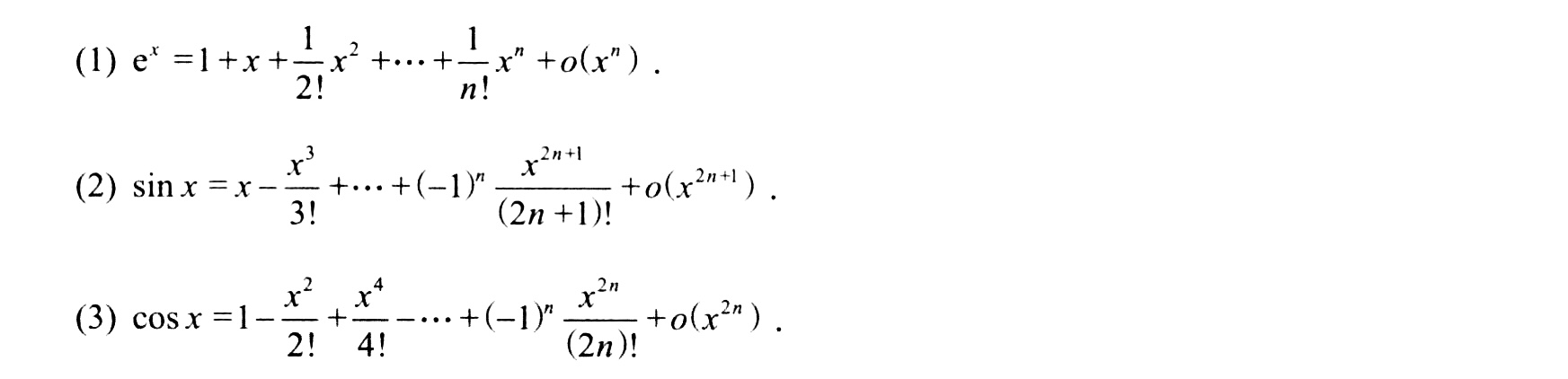
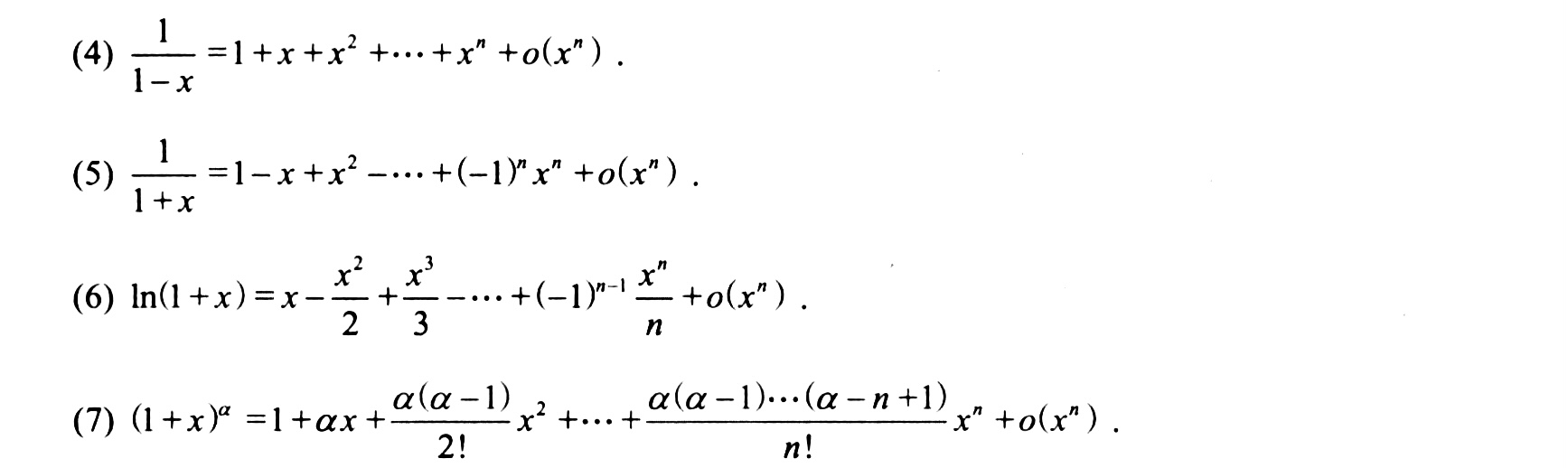
牛顿插值法
Tip
与泰勒公式结合,加深对泰勒公式的理解
已知两个点的信息,求中间值。也是多项式拟合。
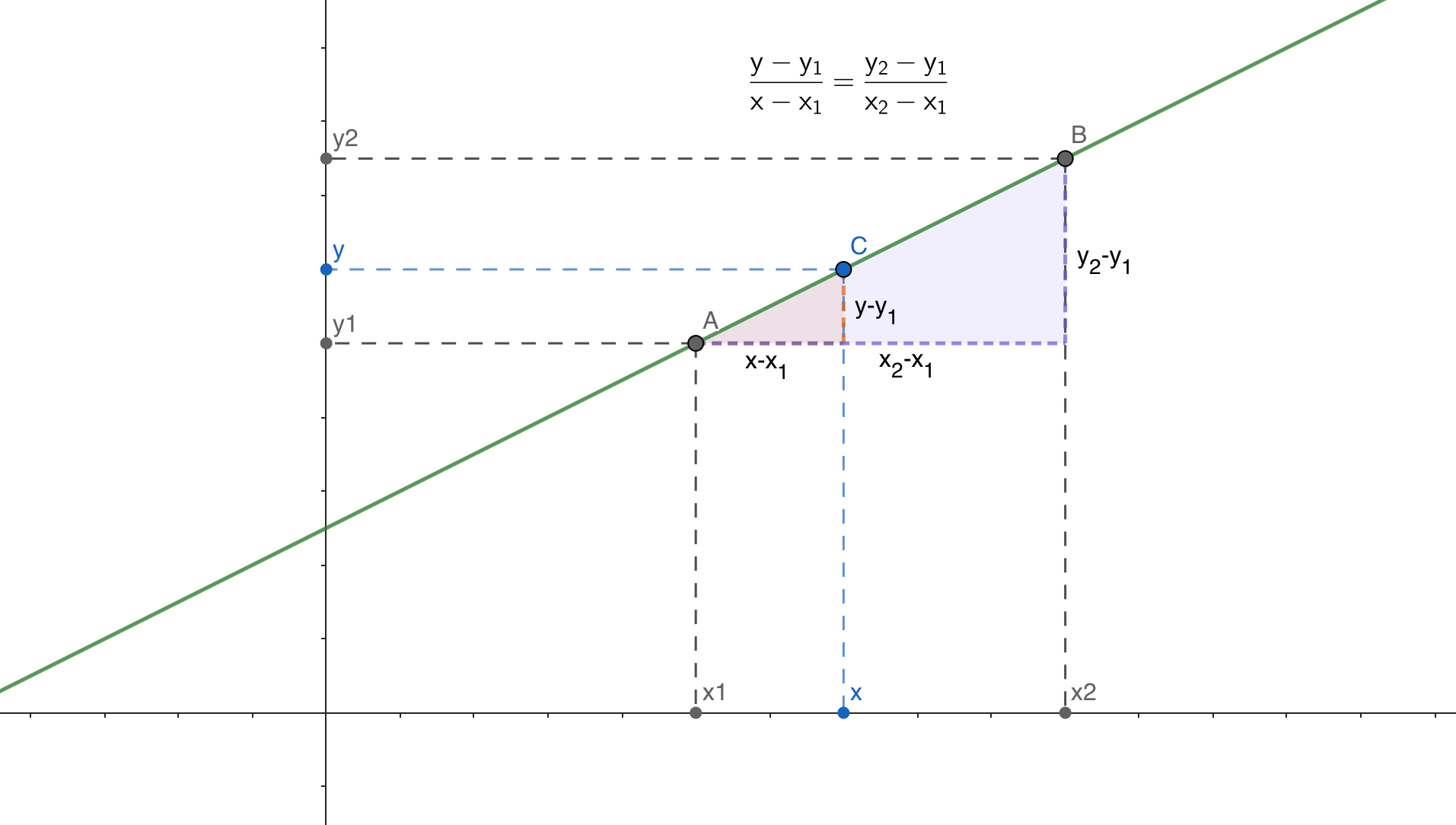
令
Info
因为为线性插值,误差较大,因此加上一个补充项
然后将中间某点代入,反解求出 。
涉及函数的定理
积分中值定理
Info
见 积分中值定理

