邻域
δ 邻域
在二维平面内的 δ 邻域是关于一个点 P0(x0,y0) 的。所有和该点的 距离 小于某正数 δ 的点的全体,称为 点 P0 的 δ ,记为 U(P0,δ)。
U(P0,δ)={P∣ ∣PP0∣<δ}
或 U(P0,δ)={(x,y)(x−x0)2+(y−y0)2<δ}
去心 δ 邻域
不包含 P0 点的 δ 邻域。
U˚(P0,δ)={P∣ 0<∣PP0∣<δ}
如果不需要强调邻域的半径 δ ,则其去心邻域记作 U˚(P0)。
极限
联系一元函数的
若:
- 函数 f(x,y) 在区域 D 上有定义;
- P0 在区域内或边界上;
- 对于 ∀ ε>0 ,总 ∃ δ>0 ,且满足 0<∣PP0∣<δ :
- 恒有 ∣f(x,y)−A∣<ε
则称常数 A 为 (x,y)→(x0,y0) 时 f(x,y) 的极限,记作:
lim(x,y)→(x0,y0)f(x,y)=A
或: x→x0y→y0limf(x,y)=A
也常记作: limP→P0f(P)=A
这种极限我们一般称之为:二重极限。
- 一元函数的极限只有两种趋近方式(正负),但在多元函数里面有无数种趋近方式(弯弯绕绕);
- 若两种趋近方式得出的值不相等,或某一路径极限值不存在,则极限不存在;
- 除 洛必达法则和 单调有界准则 以外,可照搬一元函数求极限的方法求二重极限,如
- 唯一性;
- 局部有界性;
- 局部保号性;
- 运算规则;
- 脱帽法。
- 等价无穷小 替换、夹逼准则 等技巧也是可以用的。
连续
如果 x→x0y→y0limf(x,y)=f(x0,y0) ,则称函数在 (x0,y0) 点连续。
如果函数在区域上每个点都连续,则函数在区域上连续。
偏导数
定义
函数 z=f(x,y) 在点 (x0,y0) 某邻域有定义,如果极限:
limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)
存在,则此极限为函数在 (x0,y0) 处对 x 的偏导数,记作
∂x∂zx=x0y=y0, ∂x∂fx=x0y=y0, zx′x=x0y=y0 或 fx′(x0,y0)
即:fx′(x0,y0)=limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)
偏导函数
若 z=f(x,y) 在区域 D 上的每一点都有偏导数,则偏导数的集合(一般来说也是 x,y 的函数)称为 f(x,y) 的偏导函数,简称偏导数,记作:
∂x∂z, ∂x∂f, fx′(x,y)
y 同理。
可视化解释(几何意义)
- 一元导数 → 单一方向上的变化率
- 方向导数 → 任意方向上的变化率 → 偏导数
想象从山顶上向下走,如何找到最快的路径?
计算每个方向的导数,寻找最快下降的路线。
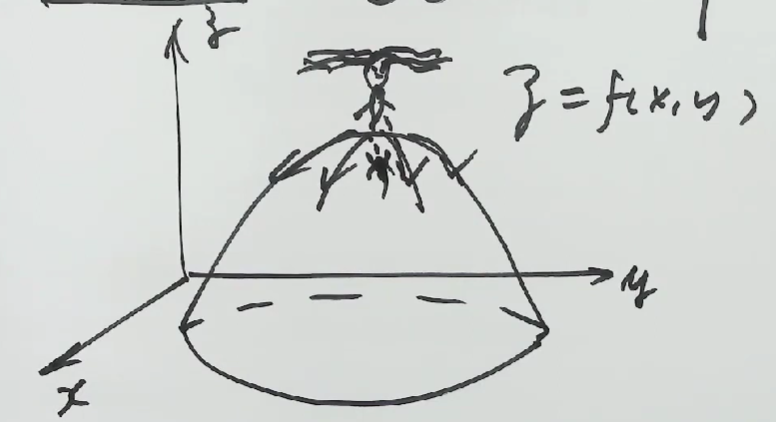
偏导数只考虑沿 x 轴或沿 y 轴的变化率,是方向导数的特殊情况。
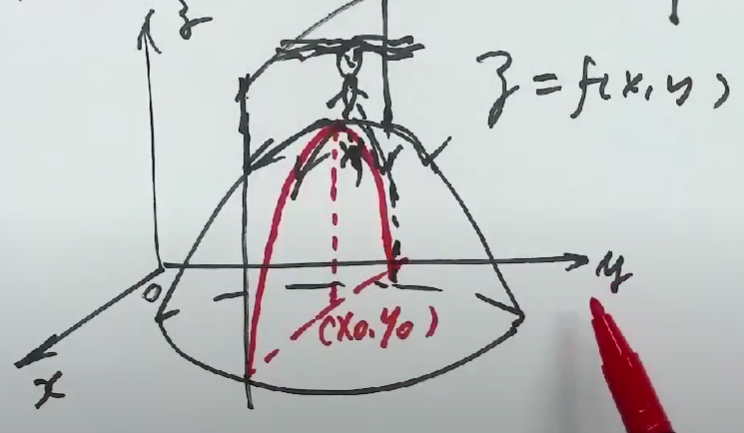
用 x 轴或 y 轴平行平面和曲面相交,得到一条交曲线,再对该曲线进行研究。
高阶偏导数
若二元函数 z=f(x,y) 的偏导数仍有偏导数,则称之为二阶偏导数。
∂x2∂2z=∂x∂(∂x∂z)=fxx′′(x,y)=zxx′′
∂x∂y∂2z=∂y∂(∂x∂z)=fxy′′(x,y)=zxy′′
对应的还有 fyy′′,fyx′′ ,此处不再赘述。
其中 fxy′′ , fyx′′ 称为二阶混合偏导数。类似的可以定义 n(n≥3) 阶偏导数。
简化
如果 z=f(x,y) 的两个二阶混合偏导数 fxy′′ , fyx′′ 都在区域连续,则区域内: fxy′′=fyx′′ 即:二阶混合偏导数在连续的条件下与求导的顺序无关。
- 求一点处的偏导数一般使用定义法;
- 求区域内偏导数一般使用公式法。
可微
把正方形 x 换成长方形 x,y :
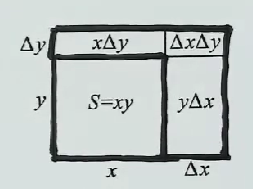
面积的增量为: ΔS=(x+Δx)(y+Δy)−xy=yΔx+xΔy+ΔxΔy
其由两部分组成:
- yΔx+xΔy :他是关于 Δx,Δy 的线性函数;
- ΔxΔy :他是比 ρ=(Δx)2+(Δy)2 的高阶无穷小量。即:
ΔS=yΔx+xΔy+o(ρ)(ρ→0)
- yΔx+xΔy 是 ΔS 的主要部分;
- o(ρ) 是 ΔS 与 yΔx+xΔy 之间的误差;
- 称 yΔx+xΔy 为函数 S=xy 在点 (x,y) 处的全微分。
定义
设函数 z=f(x,y) 在点 (x,y) 的某实心邻域有定义,若该点的全增量 Δz=f(x+Δx,y+Δy)−f(x,y) 可表示为 Δz=AΔx+BΔy+o(ρ) 其中 A,B 仅与点 (x,y) 有关而与 Δx,Δy 无关; ρ=(Δx)2+(Δy)2,且当 Δx→0,Δy→0 时, o(ρ) 为 ρ 的高阶无穷小,则称:
- 函数 z=f(x,y) 在点 (x,y) 处可微分;
- AΔx+BΔy 为函数 z=f(x,y) 在点 (x,y) 处的全微分,记为:dz=AΔx+BΔy
联系一元微分:
- Δy=f(x+Δx)−f(x) :二元的情况也是一样的,只不过两个自变量都增加;
- Δy=AΔx+o(Δx) :也是主要部分+距离 Δx 的高阶无穷小,但是二元的高阶无穷小是两个变量的距离了;
- 二元因为有两个自变量,所以叫 全 微分。
可微的必要条件
若函数 z=f(x,y) 在点 (x,y) 处可微,则该点偏导数必存在,且 A=∂x∂z,B=∂y∂z
由此可得,若函数 z=f(x,y) 在点 (x,y) 处可微,则全微分可记为:
dz=∂x∂zdx+∂y∂zdy
切线 → 切平面,各个方向的变化率
可以用平面上的点的值代替曲面上的点的值
全增量=线性增量+高阶无穷小(高度差)
可微的充分条件
若函数 z=f(x,y) 在点 (x,y) 处的偏导数存在且连续,则该函数在点 (x,y) 处可微。
- 区域上,若全微分为 0 ,则区域上 f(x,y)=C (常数)
- 判别函数在点 (x0,y0) 处偏导数是否连续步骤如下:
- 定义法求 fx′(x0,y0),fy′(x0,y0);
- 公式法求 fx′(x,y),fy′(x,y)
- 计算 x→x0y→y0limfx′(x,y),x→x0y→y0limfy′(x,y)
- 若 x→x0y→y0limfx′(x,y)=fx′(x0,y0),x→x0y→y0limfy′(x,y)=fy′(x0,y0),则在该点偏导数连续。
- 一元函数和多元函数在极限存在、连续、可导、可微的联系与区别:

可微的判别步骤
判别函数 z=f(x,y) 在点 x0,y0 处是否可微:
- 写出全增量 Δz=f(x0+Δx,y0+Δy)−f(x0,y0);
- 写出线性增量 AΔx+BΔy,其中 A=fx′(x0,y0),B=fy′(x0,y0);
- 作极限 Δx→0Δy→0lim(Δx)2+(Δy)2Δz−(AΔx+BΔy),若极限等于 0 (是高阶无穷小),则在该点可微。



