多元函数的极值与最值

Tldr

多元微分的应用

概念

理想状态下：如果该点是顶点，则其切平面一定垂直于水平面；任何一条切线也 必须水平。

点 $(x_0,y_0)$ 的某个邻域有 $f(x,y)\le f(x_0,y_0)或f(x,y)\ge f(x_0,y_0)$ 则点 $(x_0,y_0)$ 为 $f(x,y)$ 的极大（小）值点。

最值将邻域变成 定义域 即可。

Note

某一点比周围的函数值点不小，则该点是极大值点。（局部）

极大/小值不需要该点连续/可微。（考虑圆锥顶点）

联系一元函数 极值的定义 最值或取值范围

无条件极值

二元函数取极值的必要条件

Note

类比一元函数； 同样可以类比三元及以上函数

设 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处：

• 一阶偏导数存在，
• 取极值，

则 $f_x^{\prime }(x_0,y_0)=0$， $f_y^{\prime }(x_0,y_0)=0$

Caution

切线水平只是必要条件，不是充分条件； 偏导数不存在的点也可以是极值点。（圆锥顶点）

二元函数取极值的充分条件

记：

• $f_{xx}^{\prime \prime }(x_0,y_0)=A,$
• $f_{xy}^{\prime \prime }(x_0,y_0)=B,$
• $f_{yy}^{\prime \prime }(x_0,y_0)=C,$

则 $\Delta =AC-B^2$

• $\Delta >0\Rightarrow$ 极值：
  • $A<0\Rightarrow$ 极大值；
  • $A>0\Rightarrow$ 极小值；
• $\Delta <0\Rightarrow$ 非极值；
• $\Delta =0\Rightarrow$ 方法失效，另谋他法。

Caution

该方法不适用于三元及三元以上的函数。

Note

• 如何记忆：开不开心少年团、大胡子爷爷、小哑巴猪。
• 如何使用：先使用必要条件求出所有可疑点，再用充分条件判断可疑点是否是极值点
• 例 13.19

Example

条件最值与拉格朗日乘数法

求目标函数 $u=f(x,y,z)$ 在约束条件：

• $\phi (x,y,z)=0$
• $\psi (x,y,z)=0$

下的最值，则

1. 构造辅助函数 $F(x,y,z,\lambda ,\mu )=f(x,y,z)+\lambda \phi (x,y,z)+\mu \psi (x,y,z)$
2. 令

F_x' = f_x' + \lambda \varphi_x' + \mu \psi_x' = 0 \\ F_y' = f_y' + \lambda \varphi_y' + \mu \psi_y' = 0 \\ F_z' = f_z' + \lambda \varphi_z' + \mu \psi_z' = 0 \\ F_\lambda' = \varphi (x,y,z) = 0 \\ F_\mu' = \psi (x,y,z) = 0 \end{matrix}\right.

3. 解出方程组得到备选点 $P_i,i=1,2,3,\cdots ,n$ ，并求 $f(P_i)$，取最大最小值 $u_{max},u_{min}$
4. 根据实际问题，必存在最值，所得即为所求。

Note

• $\lambda ,\psi$ 是拉格朗日乘数。
• 有点类似线性组合，但 $\lambda ,\psi$ 不是常量而是变量，只是形式相似。
• $辅助函数变量数=目标函数变量数+约束个数$ 。不一定是 $3+2$，根据实际题目变通。
• 对辅助函数求每个自变量偏导，等于 $0$ 。
• 写出偏导数就能拿 5 分，几乎是白送。
• 后续才是难点，求解完成可再拿 7 分。

最远（近）点的垂线原理

Note

• 可以直接使用。
• 有可能会在多元最值上节约大量时间，提高解题效率。

如果 $\Gamma$ 是光滑闭曲线，点 $Q$ 是 $\Gamma$ 外一点，点 $P_1,P_2$ 是曲线上距离 $Q$ 的最远和最近点，则：

直线 $PQ$ 垂直 $P$ 点处切线。

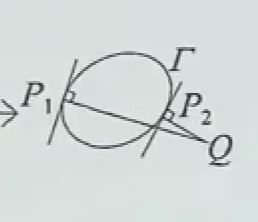
若两条不相交光滑闭曲线 ${\Gamma }_1,{\Gamma }_2$ ， $P_1,P_2$ 分别是最远（近）点，则：

直线 $P_1{P}_2$ 是 ${\Gamma }_1,{\Gamma }_2$ 的公垂线。

Example

再代入方程即可得

有界闭区域上连续函数的最值问题

理论依据

最大值最小值定理：有界闭区域上的多元连续函数，区域上一定有最大最小值。

求法

1. 根据 $f_x^{\prime }(x,y),f_y^{\prime }(x,y)$ 为 $0$ 或不存在，求出区域内部的所有可疑点；
2. 用 拉格朗日乘数法 或 代入法 求出边界上的所有可疑点；
3. 比较所有可疑点大小，得到最小最大值。