高阶导数

一般认为： $n\ge 2$ 为高阶导数。

归纳法

逐次求导，探索规律，得出通式。

例： 求 $y=\sin x$ 的 $n$ 阶导数。

$$\begin{array}{rl}y’=& (\sin x)’=\cos x=\sin (x+\frac{\pi }{2})\\ y^{\prime \prime }=& (\sin (x+\frac{\pi }{2}))’=\cos (x+\frac{\pi }{2}))=\sin (x+\frac{\pi }{2}+\frac{\pi }{2})\\ \cdots & \\ y^{(n)}=& \sin (x+n\cdot \frac{\pi }{2})\end{array}$$

常用高阶导数

详见常用高阶导数公式

莱布尼茨公式

设 $u=u(x),v=v(x)$ 均 $n$ 阶可导，则：

$$(u\pm v{)}^{(n)}=u^{(n)}\pm v^{(n)}$$ $$\begin{array}{rl}(uv{)}^{(n)}=& u^{(n)}v+C_n^1{u}^{(n-1)}v’+C_n^2{u}^{(n-2)}v’’+\cdots +C_n^k{u}^{(n-k)}{v}^{(k)}+\cdots +C_n^{n-1}u’v^{(n-1)}+u{v}^{(n)}\\ =& \sum _{k=0}^n{C}_n^k{u}^{(n-k)}{v}^{(k)}\end{array}$$

Caution

1. 见到求两个函数乘积的高阶导数，一般用莱布尼茨公式即可。有时要结合 归纳法。
2. 当一个函数求高阶导数较复杂时，如果能转化为乘积的形式，也可用莱布尼茨公式。

泰勒展开式

和泰勒公式同样重要！

抽象展开

任何一个无穷阶可导函数可写成：

$$y=f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n,$$

或者在 $0$ 点展开：

$$y=f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(0)}{n!}{x}^n$$

具体展开

题目给出一个具体的无穷阶可导函数 $y=f(x)$ ，可以通过 已知公式 展开为幂级数。

已知公式 熟记

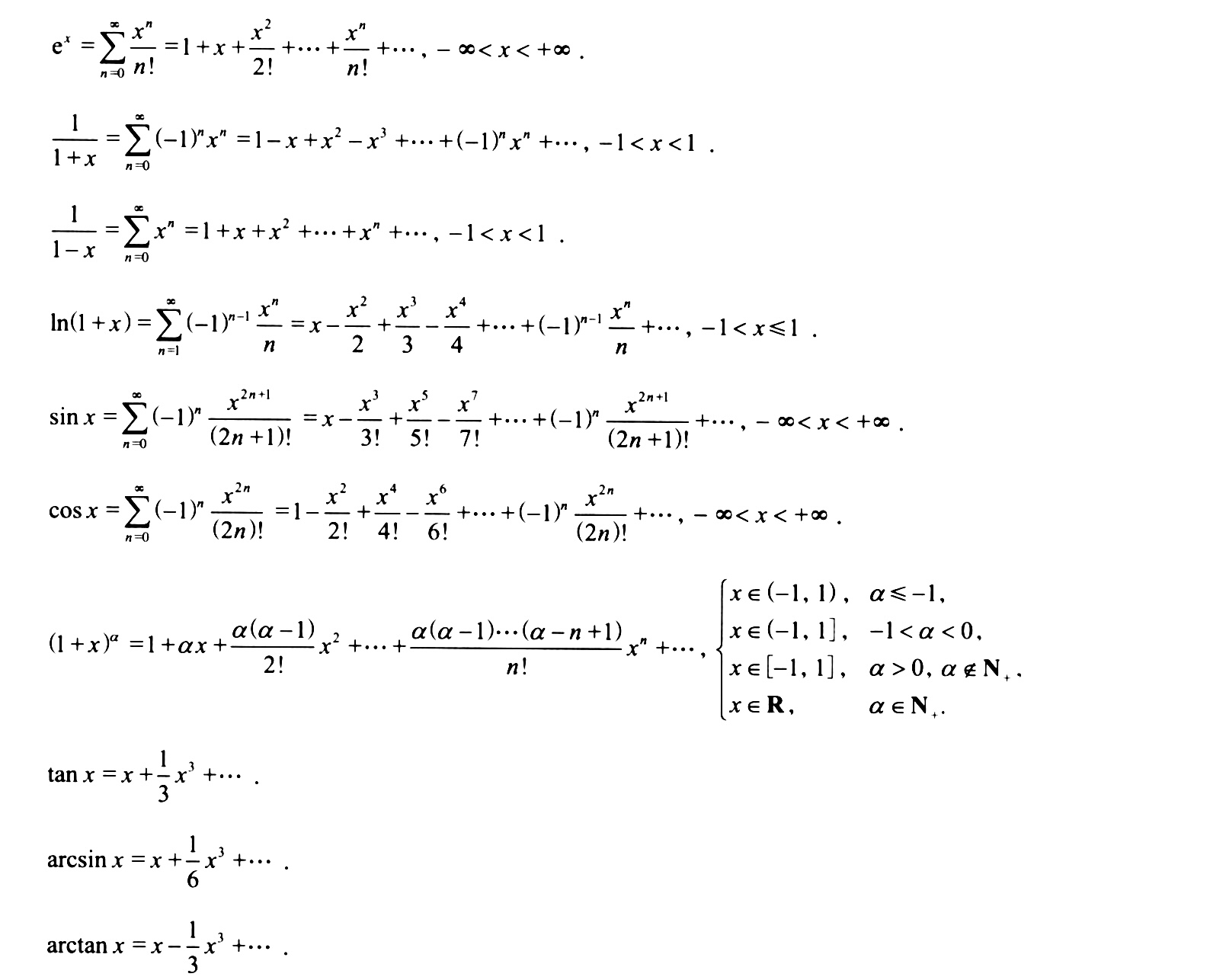
唯一性

无论 $f(x)$ 用什么方式展开，其泰勒展开式具有 唯一性。因此我们可以通过比较 抽象展开 和 具体展开 中公式的系数，获得 $f^{(n)}(x_0)$ 或者 $f^{(n)}(0)$。