二次型的定义与矩阵表示

定义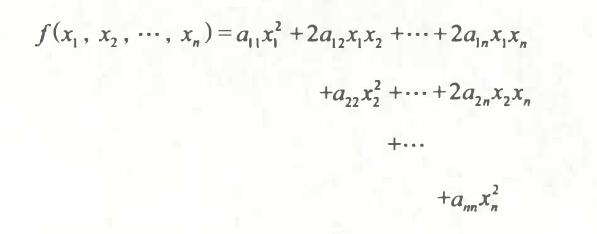

$n$ 元变量 $x_1,x_2,\cdots ,x_n$ 的二次齐次多项式 称为： $n$ 元二次型，简称二次型。

Tldr

就是未知数的次幂始终是2。例如： $f(x_1,x_2,x_3)=x_1^2+5x_2^2-4x_3^2-2x_1{x}_2+6x_2{x}_3$

Note

考研只研究系数为实数的情况，故称之为实二次型。

因为 $x_i{x}_j=x_j{x}_i$ ，若令 $a_{ij}=a_{ji}$ ，则 $2a_{ij}{x}_i{x}_j=a_{ij}{x}_i{x}_j+a_{ji}{x}_j{x}_i$ ，于是

其中 $(\star )$ 式称为完全展开式， $(\star \star )$ 式称为和式。

矩阵表示

令： $A=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right],\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ \cdots \\ x_n\end{array}\right]$

则二次型可表示为 $f(x)=x^{T}Ax(\star \star \star )$

$(\star \star \star )$ 式称为二次型 $f(x_1,x_2,\cdots ,x_n)$ 的矩阵表达式，实对称矩阵 $A$ 称为二次型 $f(x)$ 的矩阵。

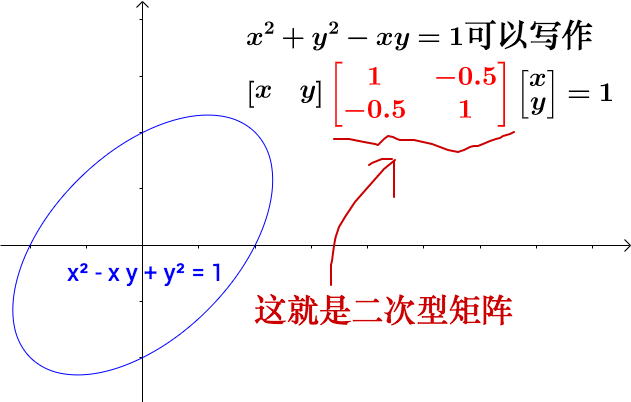
Example

Note

事实上，同一个二次型可以有不同的写法。如： $4x_1{x}_2$ 可被拆分为 $1x_1{x}_2+3x_2{x}_1$ ：$\left[\begin{array}{ccc}-& 1& -\\ 3& -& -\\ -& -& -\end{array}\right]$ 从而得出不同的二次型矩阵。

正因如此，我们要按照 规矩 将二次型矩阵化为对称矩阵，将 $4x_1{x}_2$ 写为 $2x_1{x}_2+2x_2{x}_1$ ，对称矩阵如下：$\left[\begin{array}{ccc}-& 2& -\\ 2& -& -\\ -& -& -\end{array}\right]$