级数敛散性的判别

正项级数

收敛原则

$$正项级数\sum _{n=1}^{\infty }{u}_n收敛的充要条件是其部分和数列\{S_n\}有界$$

Example

$\sum _{n=1}^{\infty }\frac{1}{n!}$

比较判别法

即大的收敛小的也收敛，小的发散大的也发散。

$$给出两个正项级数\sum _{n=1}^{\infty }{u}_n，\sum _{n=1}^{\infty }{v}_n，若从某项开始有u_n⩽v_n成立，则：$$ $$若\sum _{n=1}^{\infty }{v}_n收敛，则\sum _{n=1}^{\infty }{u}_n也收敛；若\sum _{n=1}^{\infty }{u}_n发散，则\sum _{n=1}^{\infty }{v}_n也发散。$$

Example

$\sum _{n=1}^{\infty }{a}_n收敛\Rightarrow \sum _{n=1}^{\infty }{a}_n^2收敛$

比较判别法的极限形式

$$给出两个正项级数\sum _{n=1}^{\infty }{u}_n，\sum _{n=1}^{\infty }{v}_n，v_n\ne 0，且\underset{n\to \infty }{\lim }\frac{u_n}{v_n}=A：$$ $$若A=0，则当\sum _{n=1}^{\infty }{v}_n收敛时，\sum _{n=1}^{\infty }{u}_n也收敛。$$ $$当A=+\infty ，当\sum _{n=1}^{\infty }{v}_n发散时，\sum _{n=1}^{\infty }{u}_n也发散$$ $$若0<A<+\infty ，则\sum _{n=1}^{\infty }{v}_n与\sum _{n=1}^{\infty }{u}_n具有相同敛散性。$$

Tip

$\frac{0}{0}$ 才有意义 无穷小比阶

Example

$\sum _{n=2}^{\infty }\sin (n^{-\alpha }\ln n)$

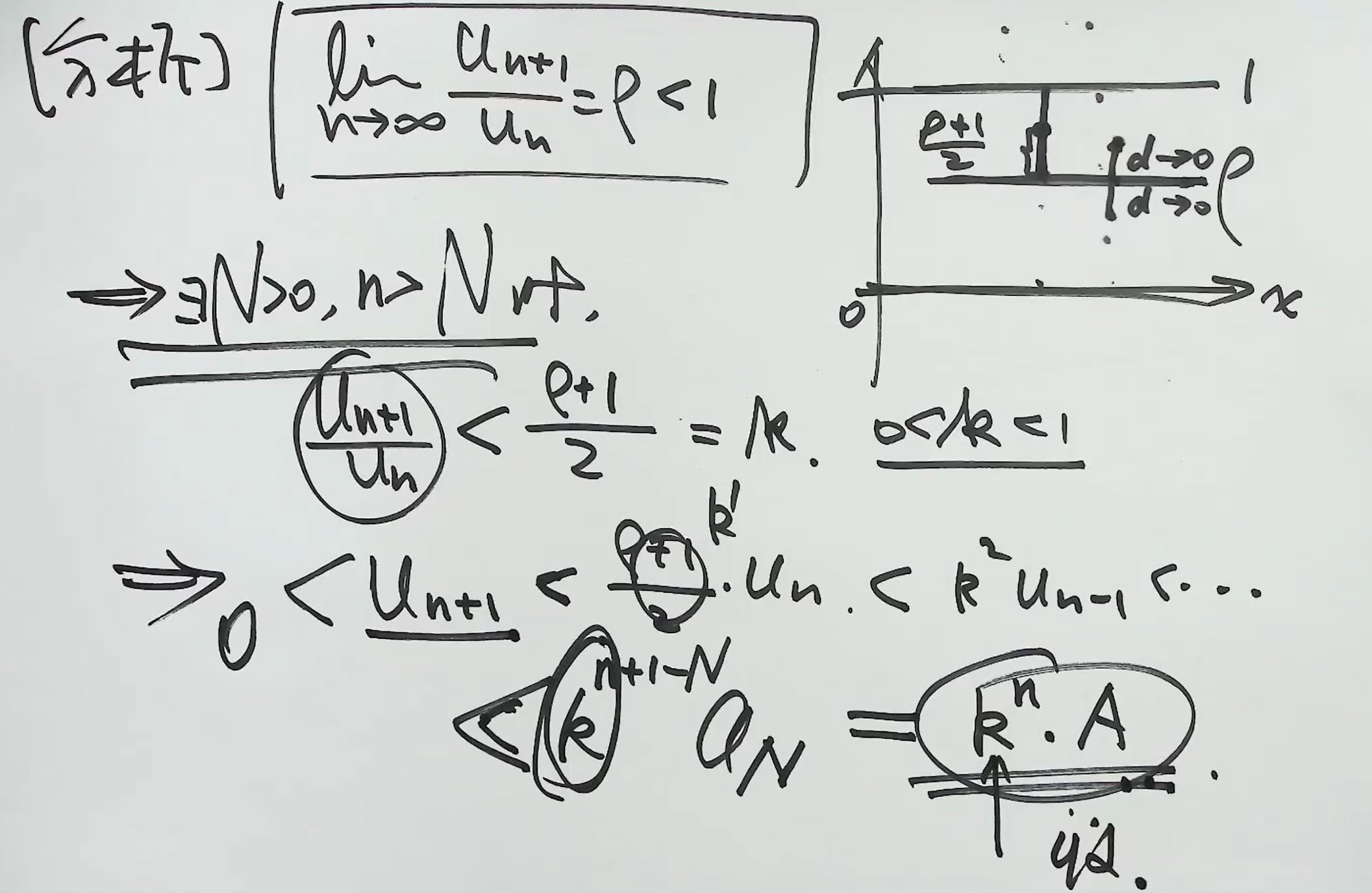
比值判别法（达朗贝尔判别法）

$$给出一正项级数\sum _{n=1}^{\infty }{u}_n，若\underset{n\to \infty }{\lim }\frac{u_{n+1}}{u_n}=\rho ，则：若\rho <1，则\sum _{n=1}^{\infty }{u}_n收敛；若\rho >1，则\sum _{n=1}^{\infty }{u}_n发散。$$

Tip

本质还是和 $k^n$ 比较 证明：

Example

$\sum _{n=1}^{\infty }\frac{a^{n}n!}{n^n}$

根值判别法（柯西判别法）

$$给出正项级数\sum _{n=1}^{\infty }{u}_n，若\underset{n\to \infty }{\lim }\sqrt[n]{u_n}=\rho ，则若\rho <1，则\sum _{n=1}^{\infty }{u}_n收敛；若\rho >1，则\sum _{n=1}^{\infty }{u}_n发散。$$

Tip

本质是和 $k^n$ 比较 证明： $\sqrt{a_n}<\frac{\rho +1}{2}=k$ $0<u_n<k^n$

积分判别法

$$设f(x)是在[1,+\infty )上单调递减且非负的连续函数，a_n=f(n)，则\sum _{n=1}^{\infty }{a}_n与{\int }_1^{+\infty }f(x)\text{d}x同敛散。$$

Note

1. ${\int }_0^1\frac{1}{x^p}\mathrm{d}x\{\begin{array}{l}\text{ 收敛, }0<p<1\\ \text{ 发散, }p\ge 1\end{array}$

2. ${\int }_1^{+\infty }\frac{1}{x^p}\mathrm{d}x\{\begin{array}{l}\text{ 收敛, }p>1\\ \text{ 发散, }p\le 1\end{array}$

3. ${\int }_2^{+\infty }\frac{1}{x{\ln }^{p}x}\mathrm{d}x\{\begin{array}{l}\text{ 收敛, }p>1\\ \text{ 发散, }p\le 1\end{array}$

4. ${\int }_2^{+\infty }\frac{1}{x^p{\ln }^{q}x}\mathrm{d}x\{\begin{array}{l}\text{ 收敛, }p>1\\ \text{ 收敛, }p=1,q>1\\ \text{ 发散, }其他\end{array}$

交错级数

概念

$$\begin{array}{rl}& 若级数各项\text{正负相间}出现，则这样的级数是\text{交错级数}，\\ & 一般写为\sum _{n=1}^{\infty }(-1{)}^{n-1}{u}_n=u_1-u_2+u_3-u_4+\cdots +(-1{)}^{n-1}{u}_n+\cdots ，其中u_n>0。\end{array}$$

莱布利兹判别法

$$\begin{array}{rl}& 给出一交错级数\sum _{n=1}^{\infty }(-1{)}^{n-1}{u}_n，u_n>0，n=1,2,\cdots ，\\ & 若\{u_n\}\text{单调不增}{u}_n⩾u_{n+1}且\underset{n\to \infty }{\lim }=0，则该级数收敛。反过来则不行。\end{array}$$

Note

1. $\{u_n\}单调减少$
2. $u_{n+1}-u_n$，$\frac{u_{n+1}}{u_n}$
3. $u_n=f(n)\to f(x)\to f^{\prime }(x)$
4. 如果 $\{u_n\}$ 无单调性

• 拆项

任意项级数

$$\begin{gathered} \text{定义：}设\sum _{n=1}^{\infty }{u}_n为任意项级数，若\sum _{n=1}^{\infty }|u_n|收敛，则称\sum _{n=1}^{\infty } \\ {u}_n\text{绝对收敛}。 \end{gathered}$$ $$\begin{gathered} \text{定义：}设\sum _{n=1}^{\infty }{u}_n为任意项级数，若\sum _{n=1}^{\infty }{u}_n收敛，但\sum _{n=1}^{\infty } \\ |u_n|发散，则称\sum _{n=1}^{\infty }{u}_n\text{条件收敛}。 \end{gathered}$$

注：

$$若\sum _{n=1}^{\infty }\mid u_n\mid 收敛，则\sum _{n=1}^{\infty }{u}_n必收敛$$

证明

$0\le \mid u_n\mid +u_n\le 2\mid u_n\mid$

注1

对于任意项级数 $\sum _{n=1}^{\infty }{u}_n$，引入级数 $\sum _{n=1}^{\infty }{v}_n$ 和 $\sum _{n=1}^{\infty }{w}_n$

$$v_n=\frac{1}{2}(u_n+\mid u_n\mid )=\{\begin{array}{ll}{u}_n& u_n>0\\ 0& u_n\le 0\end{array}$$ $$w_n=\frac{1}{2}(\mid u_n\mid -u_n)=\{\begin{array}{ll}-u_n& u_n<0\\ 0& u_n\ge 0\end{array}$$

$\sum _{n=1}^{\infty }{v}_n$ 为全体正项所构成的级数，$\sum _{n=1}^{\infty }{w}_n$ 为全体负项的绝对值构成的级数

• 如果级数 $\sum _{n=1}^{\infty }{u}_n$ 绝对收敛，则 $\sum _{n=1}^{\infty }{v}_n$ 和 $\sum _{n=1}^{\infty }{w}_n$ 都收敛
• 如果级数 $\sum _{n=1}^{\infty }{u}_n$ 条件收敛，则 $\sum _{n=1}^{\infty }{v}_n$ 和 $\sum _{n=1}^{\infty }{w}_n$ 都发散
• 特别的，如果交错级数 $\sum _{n=1}^{\infty }(-1{)}^{n-1}{u}_n(u_n>0)$ 条件收敛，则 $\sum _{n=1}^{\infty }{u}_{2n-1}$ 和 $\sum _{n=1}^{\infty }-u_{2n}$ 都发散

注 2

若 $\sum _{n=1}^{\infty }{u}_n$ 和 $\sum _{n=1}^{\infty }{v}_n$ 绝对收敛，则 $\sum _{n=1}^{\infty }(u_n\pm v_n)$ 绝对收敛

注 3

若 $\sum _{n=1}^{\infty }{u}_n$ 绝对收敛， $\sum _{n=1}^{\infty }{v}_n$ 条件收敛，则 $\sum _{n=1}^{\infty }(u_n\pm v_n)$ 条件收敛

注 4

若 $\sum _{n=1}^{\infty }{u}_n$ 和 $\sum _{n=1}^{\infty }{v}_n$ 均条件收敛，则 $\sum _{n=1}^{\infty }(u_n\pm v_n)$ 收敛

注 5

如果级数 ${\sum }_{n=1}^{\infty }\mid u_n\mid$ 发散，我们不能断定级数 $\sum _{n=1}^{\infty }{u}_n$ 是否发散，但是如果我们用的是比值判别法或根值判别法得出的 $\rho >1$ 而判定级数 ${\sum }_{n=1}^{\infty }\mid u_n\mid$ 发散的，那么我们可以判定级数 $\sum _{n=1}^{\infty }{u}_n$ 也发散。 这是因为从ρ>1 可推知 ${\lim }_{n\to \infty }|u_n|\ne 0$，从而 ${\lim }_{n\to \infty }{u}_n\ne 0$，因此级数 ${\sum }_{n=1}^{\infty }{u}_n$ 是发散的。

注 6

交错 $p$ 级数

$$\sum _{n=1}^{\infty }(-1{)}^{n-1}\frac{1}{n^p}\{\begin{array}{ll}绝对收敛，& p>1\\ 条件收敛，& 0<p\le 1\end{array}$$

抽象数项级数的判别